线段树详解

线段树的二三事

线段树有什么用？

作为一个比较复杂的数据结构能有如此的知名度，线段树一定有它的拿手绝活， 那么线段树能做什么呢？

简而言之，线段树可以高效地维护区间上对于某个操作结果的信息， 但这个操作必须符合结合律.

最有名的应用就是区间和。当然区间积，最值 (也可以用 ST 表) 也是可以的.

注意：线段树不支持动态添加节点， 因此如果需要修改区间长度的场合不能用线段树

线段树长什么样

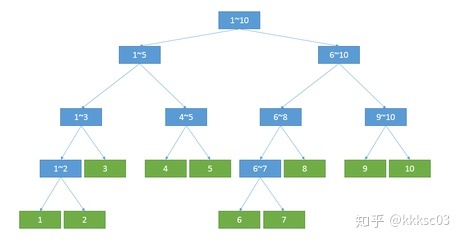
从图上可以看出，线段树就是一颗二叉树. 其中的节点管理着一定区间内对应操作的结果. 父节点管理的区间是两个子结点管理的区间的并集. 子节点不断向自己的父亲节点传递信息， 而父节点存储的信息则是他的每一个子节点信息的整合.

线段树就是分块思想的树化， 或者说是对于信息处理的二进制化 -- 用于达到 O (logn) 级别的处理速度.

分块的思想，则可以用一句话总结为: 通过将整个序列分为有穷个小块，对于要查询的一段区间， 总是可以整合成 k 个所分块与 m 个单个元素的信息的并 ()(). 但普通的分块不能高效率地解决很多问题，所以作为 log 级别的数据结构， 线段树应运而生.

分块的应用范围还是要广于线段树的，因为虽然线段树好像很快，但是它只能维护带有结合律的信息，比如区间 max/min、sum、xor 之类的，但是不带有结合律的信息就不能维护（且看下文分解）；而分块则灵活得多，可以维护很多别的东西，因为实际上分块的本质就是优雅的暴力

我们先定义几个线段树实现中必须的查找函数

inline long long get_mid(long long left_to_manage, long long right_to_manage){
    return (right_to_manage - left_to_manage) >> 1 + left_to_manage;
}
inline long long get_left_child(long long position){
    return position << 1;
}
inline long long get_right_child(long long position){
    return position << 1 + 1;
}

def get_mid(left_to_manage, right_to_manage):
    return (right_to_manage + left_to_manage) // 2
def get_left_child(position):
    return position // 2 + 1
def get_right_child(position):
    return position // 2 + 2

线段树怎么建

虽然名字叫线段树，但是因为是平衡二叉树，实现的时候常常使用数组.

建树的时候，因为父节点的值又两个子结点决定，因此可以递归建树， 先建好子结点，然后再根据子结点建父节点

void build(long long left, long long right, long long position)
{
    if(left == right){
        segment_tree[position] = array[left];
        return;
    }
    long long middle = get_mid(left_to_manage, right_to_manage)
    build(left, middle, get_left_child(position));
    build(middle+1, right, get_right_child(position));
    push_up(position);
}

void push_up(long long position){
    // 区间和时的实现
    segment_tree[position] = segment_tree[get_left_child(position)] + segment_tree[get_right_child(position)];
}

void push_up(long long position){
    // 区间极值时的实现
    segment_tree[position] = min(segment_tree[get_right_child(position)], segment_tree[get_right_child(position)]);
}

def build(left, right, position):
    if left == right:
        segment_tree[position] = array[position]
        return

    middle = get_mid(left_to_manage, right_to_manage)

    build(left, middle, get_left_child(position))
    build(middle+1, right, get_right_child(position))
    push_up(position)

def push_up(position):
    """
        区间和时的实现
    """
    segment_tree[position] = segment_tree[get_left_child(position)] + segment_tree[get_right_child(position)]

def push_up(position):
    """
        区间最小值时的实现
    """
    segment_tree[position] = min(segment_tree[get_left_child(position)], segment_tree[get_right_child(position)])

如何实现区间修改， 以及用懒标记优化它

区间修改可是个麻烦事，因为一个地方改了， 所有管理区间和这个地方有交集的节点的值都需要修改.

因此我们引入懒标记，被打上懒标记代表这个节点的 子结点 没有增加 对应的值.

懒标记需要在适当时间传递下去，我们先完成一个传递函数.

void push_down(long long position, long long len)
{
    tags[get_left_child(position)] += tags[position];
    tags[get_right_child(position)] += tags[position];
    segment_tree[get_left_child(position)] += tags[position] * (len - len / 2);
    segment_tree[get_right_child(position)] += tags[position] * (len / 2); // 右边的区间可能要短一点
    tags[position] = 0;
}

def push_down(position, length):
    tags[get_left_child(position)] += tags[position]
    tags[get_right_child(position)] += tags[position]
    segment_tree[get_left_child(position)] += tags[position] * (length - length / 2)
    segment_tree[get_right_child(position)] += tags[position] * (length / 2) # 右边区间可能要短一点
    tags[position] = 0

然后，对于每个节点 position, 它管理区间 [left_to_manage, right_to_manage], 和待修改区间 [left_to_change, right_to_change] 之间只可能有三种关系.

---

第一种，left_to_manage > right_to_change 或 right_to_manage left_to_change, 即管理区间和待修改区间没有关系.

这种没什么好说的，直接返回即可.

---

第二种，left_to_manage left_to_change 且 right_to_manage right_to_change, 即管理区间被待修改区间包含.

这种直接更新 position 的值，然后给 position 打上懒标记.

segment_tree[position] += (right_to_change - left_to_change + 1) * value
tags[position] += value

---

第三种，其它情况.

这时候我们递归到子结点中处理，最后收集子结点的值更新父节点.
对了，不要忘记把懒标记传递给子结点

middle = get_mid(left_to_manage, right_to_manage)
push_down(position, right_to_manage - left_to_manage + 1)
range_modify(get_left_child(position) left_to_manage, middle, left_to_change, right_to_change, value)
range_modify(get_right_child(position) ,middle + 1, right_to_manage, left_to_change, right_to_change, value)
push_up(position)

---

整合三种情况

void range_modify(
    long long position,
    long long left_to_manage,
    long long right_to_manage,
    long long left_to_change,
    long long right_to_change,
    long long value){
    if(left_to_manage > right_to_change || right_to_manage < left_to_change) return;
    if(left_to_manage >= left_to_change && right_to_manage <= right_to_change){
        segment_tree[position] += (right_to_manage - left_to_manage + 1) * value;
        tags[position] += value;
    } else {
        long long middle = get_mid(left_to_manage, right_to_manage)
        push_down(position, right_to_manage - left_to_manage + 1);
        range_modify(get_left_child(position), left_to_manage, middle, left_to_change, right_to_change, value);
        range_modify(get_right_child(position) ,middle + 1, right_to_manage, left_to_change, right_to_change, value);
        push_up(position);
    }
}

def range_modify(position, left_to_manage, right_to_manage, left_to_change, right_to_change, value):
    if left_to_manage > right_to_change or right_to_manage < left_to_change: return
    if left_to_manage >= left_to_change and right_to_manage <= right_to_change:
        segment_tree[position] += (right_to_manage - left_to_manage + 1) * value
        tags[position] += value
    else:
        middle = get_mid(left_to_manage, right_to_manage)
        push_down(position, right_to_manage - left_to_manage + 1)
        range_modify(get_left_child(position), left_to_manage, middle, left_to_change, right_to_change, value)
        range_modify(get_right_child(position), middle + 1, right_to_manage, left_to_change, right_to_change, value)
        push_up(position)

如何实现区间查询

基本等同于区间修改，只是由更新值变成获取值返回.

long long query(
    long long position,
    long long left_to_manage,
    long long right_to_manage,
    long long left_to_change,
    long long right_to_change
{
    if (right_to_change < left_to_manage || left_to_change > right_to_manage)
        return 0;
    else if (left_to_change <= left_to_manage && right_to_change >= right_to_manage)
        return segment_tree[position];
    else
    {
        long long middle = get_mid(left_to_manage, right_to_manage)
        push_down(position, right_to_manage - left_to_manage + 1);
        return query(position >> 1 + 1, left_to_manage, middle, left_to_change, right_to_change) + query(position >> 1 + 2, middle + 1, right_to_manage, left_to_change, right_to_change);
    }
}

def query(position, left_to_manage, right_to_manage, left_to_change, right_to_change):
    if right_to_change < left_to_manage or left_to_change > right_to_manage:
        return 0
    elif left_to_change <= left_to_manage && right_to_change >= right_to_manage:
        return segment_tree[position]
    else:
        middle = get_mid(left_to_manage, right_to_manage)
        push_down(position, right_to_manage - left_to_manage + 1)
        return query(position >> 1 + 1, left_to_manage, middle, left_to_change, right_to_change) + query(position >> 1 + 2, middle + 1, right_to_manage, left_to_change, right_to_change)

一些小 tips

• 同时维护区间乘和区间加两个懒标记时， 记得处理成先乘后加避免引入浮点数.

引用

浅谈线段树
算法学习笔记 (14): 线段树